複素数

一応、複素数の基礎から復習します。ここはpython入門ですので、複雑な数式はなしでなるべくプログラミングベースで説明します。また複素数の実部、虚部はfloat型ですので【python】float型オブジェクトで述べたのと同様、complexの計算でも誤差が発生します。

純虚数

二乗したら-1になる数を虚数単位といい数学上はiとしてあらわします。 工学系ではiではなくjであらわす事が多いです。 pythonではiではなくjを用います。 数字の後にjをつけると虚数としてあらわされます。

c1=1.0j
print(c1)

実行結果

1j

純虚数ですので二乗すると以下のように-1になります。

c1=1.0j
c2=c1*c1
print(c2)

実行結果

(-1+0j)

このように実部が-1, 虚部が0(つまり実数の-1と同等)になっているのがわかります。

虚数同士の掛け算ですので、結果も虚数で表示されています。結果が実数になっても虚数の型が勝手に実数になることはありません。

↑目次

複素数の基礎

複素数は(実部+虚部×虚数単位)であらわされる数です。図であらわす時には複素平面と呼ばれる平面であらわす事が多いです。

例えば(3+4j)は実部が3、虚部が4の複素数で下図のようになります。

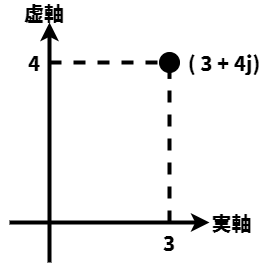
また原点(0+0j)からの距離を絶対値といいます。絶対値はabs関数で求めることができます。

以上をpythonのコードで記述すると以下のようになります。

c1=(3+4j)
# 複素数を表示
print(c1)
# 複素数の実部を表示
print(c1.real)
# 複素数の虚部を表示
print(c1.imag)
# 複素数の絶対値(原点からの距離)を表示
print(abs(c1))

実行結果

(3+4j)
3.0
4.0
5.0

 

↑目次

加減算

複素数の加減算はベクトルの加減算と同じです。下図(1+3j)と(2+1j)という2つのベクトルがあります。これを足し合わせた結果は実部は実部同士、虚部は虚部同士を足し合わせた数(3+4j)が加算の結果となります。

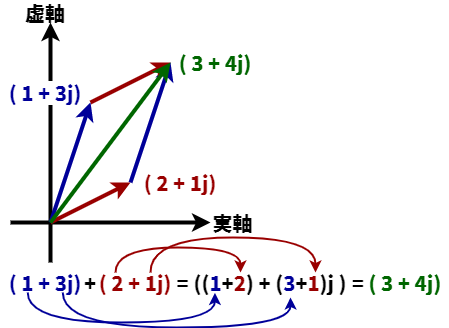
ソースコードで書くと以下の通りです。

c1=(1+3j)
c2=(2+1j)
c3=c1+c2
print(c3)

実行結果

(3+4j)

減算(引き算)の場合には引く複素数の複素数平面上で同じ大きさで逆向きのベクトル同士を足し合わせるのと同じとなります。 計算をおこなう場合には実部同士、虚部同時で引き算をおこないます。 例えば(1+3j)-(2+1j)=((1-2)+(3-1)j)=(-1+2j)となります。

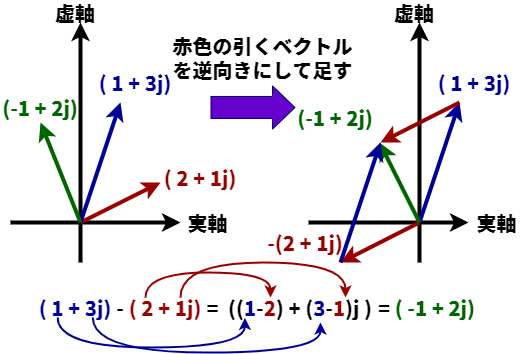
ソースコードで書くと以下の通りです。

c1=(1+3j)
c2=(2+1j)
c3=c1-c2
print(c3)

実行結果

(-1+2j)

↑目次

乗算

複素数同士での掛け算は複素数平面上では原点を中心とした回転と拡大(もしくは縮小)となります。

実際に計算する際には、分配法則に沿って計算します。

例えば(1+3j)×(2+1j)を考えます。分配法則により((1×2)+(1×1j)+(3×2j)+(3j×1j))となります。j×j=-1であることを考慮すると。(2+1j+6j-3)=(-1+7j)となります。

図にすると以下のようになります。

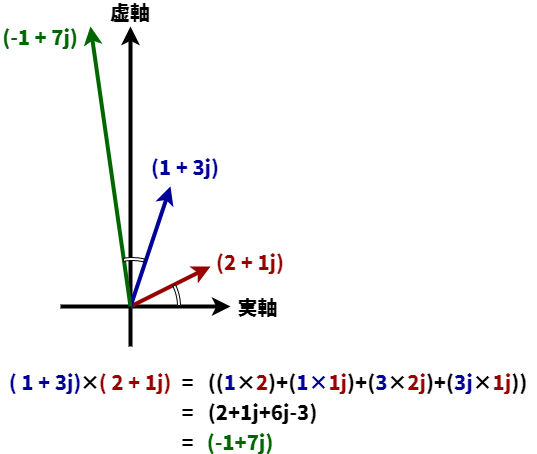
ここで計算結果の(-1+7j)の長さは元の(1+3j)の長さに(2+1j)の長さをかけた長さになっています。また実軸との角度は(1+3j)の実軸との角度に(2+1j)の実軸との角度を足し合わせた(回転させた)角度になっています。

実際にソースコードでみてみると以下の通りとなります。

from cmath import phase
c1=(1+3j)
c2=(2+1j)
c3=c1*c2
print("c1の長さ(絶対値){}".format(str(abs(c1))))
print("c2の長さ(絶対値){}".format(str(abs(c2))))
print("c3の長さ(絶対値){}".format(str(abs(c3))))
print("c1と実軸のなす角度(偏角){}".format(str(phase(c1))))
print("c2と実軸のなす角度(偏角){}".format(str(phase(c2))))
print("c3と実軸のなす角度(偏角){}".format(str(phase(c3))))
print("c3={}".format(str(c3)))

実行結果

c1の長さ3.1622776601683795
c2の長さ2.23606797749979
c3の長さ7.0710678118654755
c1と実軸のなす角度(偏角)1.2490457723982544
c2と実軸のなす角度(偏角)0.4636476090008061
c3と実軸のなす角度(偏角)1.7126933813990606
c3=(-1+7j)

以下のようになっているのがわかります。
c3の長さ=c1 の長さ × c2の長さ
c3の偏角 = c1の偏角 + c2の偏角
角度は弧度法(ラジアン)で表示されます(180°がπ=3.14…、360°が2π=6.18…)。

↑目次

複素数を扱える関数

偏角を求めるときにも使いましたがpythonでは複素数のための数学関数モジュールであるcmathを用意しています。

どのような関数があるか知りたい場合にはcmath --- 複素数のための数学関数を確認してみてください。

↑目次

まとめ

今回は普段あまり取り扱うことがない複素数について取り上げてみました。普段取り扱わないとは言え工学計算や物理計算が必要な場合は必須知識になります。このような知識はいつ必要になるかわかりません。普段必要がない人もpythonで複素数を扱える事、複素数を扱う数学関数がいくつか用意されている事は知っていて損はないと思います。

↑目次